1. Tentukan pusat dan jari-jari lingkaran berikut :
a.
Penyelesaian :
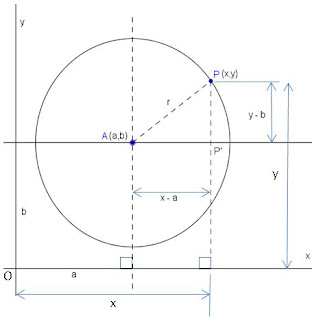
Persamaan lingkaran dengan titik pusat (a,b) dan jari-jari r adalah :
Jika persamaan lingkaran :
Jadi persamaan lingkaran
-----------------------------------
b.
Penyelesaian :
Persamaan lingkaran dengan titik pusat (a,b) dan jari-jari r adalah :
Jika persamaan lingkaran :
Jadi persamaan lingkaran
c.
-----------------------------------
Penyelesaian :
Persamaan lingkaran dengan titik pusat (a,b) dan jari-jari r adalah :
Jika persamaan lingkaran :
Jadi persamaan lingkaran
-----------------------------------
2. Tentukan persamaan lingkaran dari setiap lingkaran berikut !
a. Pusat (-3,3), jari-jari= 4.
Penyelesaian :
Persamaan lingkaran dengan titik pusat (a,b) dan jari-jari = r adalah
Jika diketahui a = -3, b = 3 dan jari-jari (r) = 4, didapatkan persamaan lingkaran :
-----------------------------------
b. Pusat (2,1), jari-jari = 6 (Selesaikan secara mandiri !).
-----------------------------------
c. Pusat (5,-2), jari-jari =
-----------------------------------
3. Tentukan persamaan dari lingkaran-lingkaran berikut :
a. Pusat (2,-3) melalui titik O.
Penyelesaian :
Melalui titik O adalah melalu titik (0,0)
a = 2 , b = -3 ,
Jadi persamaan lingkaran :
-----------------------------------
b. Pusat (3,-4) melalui titik (1,2)
Penyelesaian :
a = 3 , b = -4 ,
Jadi persamaan lingkaran :
-----------------------------------
c. Pusat (2,5), melalui titik (5,1) (Selesaikan secara mandiri !).